Struct FunnelState

int CalculateNextCornerIndices (

int	maxCorners	The maximum number of corners to add to the result array. Should be positive.
NativeArray<int>	result	Output indices. Contains an index as well as possibly the RightSideBit set. Corresponds to an index of the left or right portals, depending on if RightSideBit is set. This must point to an array which is at least maxCorners long.
float3	startPoint	Start point of the funnel. The agent will move from here to the best point along the first portal.
float3	endPoint	End point of the funnel.
out bool	lastCorner	True if the final corner of the path was reached. If true, then the return value is guaranteed to be at most maxCorners - 1 (unless maxCorners = 0).

)

Calculate the shortest path through the funnel.

void CalculateNextCorners (

int	maxCorners
bool	splitAtEveryPortal
float3	startPoint
float3	endPoint
NativeList<float3>	result

)

void Clear ()

FunnelState Clone ()

void ConvertCornerIndicesToPath (

NativeArray<int>	indices
int	numCorners
bool	splitAtEveryPortal
float3	startPoint
float3	endPoint
bool	lastCorner
NativeList<float3>	result

)

void ConvertCornerIndicesToPathProjected (

UnsafeSpan<int>	indices
bool	splitAtEveryPortal
float3	startPoint
float3	endPoint
bool	lastCorner
NativeList<float3>	result
float3	up

)

void Dispose ()

FunnelState (

int	initialCapacity
Allocator	allocator

)

FunnelState (

FunnelPortals	portals
Allocator	allocator

)

bool IsReasonableToPopEnd (

float3	startPoint
float3	endPoint

)

Like IsReasonableToPopStart but for the end of the funnel.

bool IsReasonableToPopStart (

float3	startPoint
float3	endPoint

)

True if it is reasonable that the given start point has passed the first portal in the funnel.

If this is true, it is most likely better to pop the start/end portal of the funnel first.

This can be used as a heuristic to determine if the agent has passed a portal and we should pop it, in those cases when node information is not available (e.g. because the path has been invalidated).

void Pop (

bool

fromStart

)

void PopEnd ()

void PopStart ()

void Push (

bool	toStart
Vector3	newLeftPortal
Vector3	newRightPortal

)

void PushEnd (

Vector3	newLeftPortal
Vector3	newRightPortal

)

void PushStart (

float3	newLeftPortal
float3	newRightPortal

)

void Splice (

int	startIndex
int	toRemove
List<float3>	newLeftPortal
List<float3>	newRightPortal

)

float4x3 UnwrappedPortalsToWorldMatrix (

float3

up

)

void CalculatePortalIntersections (

int	startIndex
int	endIndex
NativeCircularBuffer<float3>	leftPortals
NativeCircularBuffer<float3>	rightPortals
NativeCircularBuffer<float4>	unwrappedPortals
float2	from
float2	to
NativeList<float3>	result

)

void ConvertCornerIndicesToPathProjected (

refFunnelState	funnelState
refUnsafeSpan<int>	indices
bool	splitAtEveryPortal
in float3	startPoint
in float3	endPoint
bool	lastCorner
in float3	projectionAxis
refUnsafeSpan<float3>	result
in float3	up

)

bool DifferentSidesOfLine (

float3	start
float3	end
float3	a
float3	b

)

True if a and b lie on different sides of the infinite line that passes through start and end.

void PushStart (

refNativeCircularBuffer<float3>	leftPortals
refNativeCircularBuffer<float3>	rightPortals
refNativeCircularBuffer<float4>	unwrappedPortals
ref float3	newLeftPortal
ref float3	newRightPortal
ref float3	projectionAxis

)

NativeCircularBuffer<float3> leftFunnel

Left side of the funnel.

float3 projectionAxis

If set to anything other than (0,0,0), then all portals will be projected on a plane with this normal.

This is used to make the funnel fit a rotated graph better. It is ideally used for grid graphs, but navmesh/recast graphs are probably better off with it set to zero.

The vector should be normalized (unless zero), in world space, and should never be changed after the first portal has been added (unless the funnel is cleared first).

NativeCircularBuffer<float3> rightFunnel

Right side of the funnel.

NativeCircularBuffer<float4> unwrappedPortals

Unwrapped version of the funnel portals in 2D space.

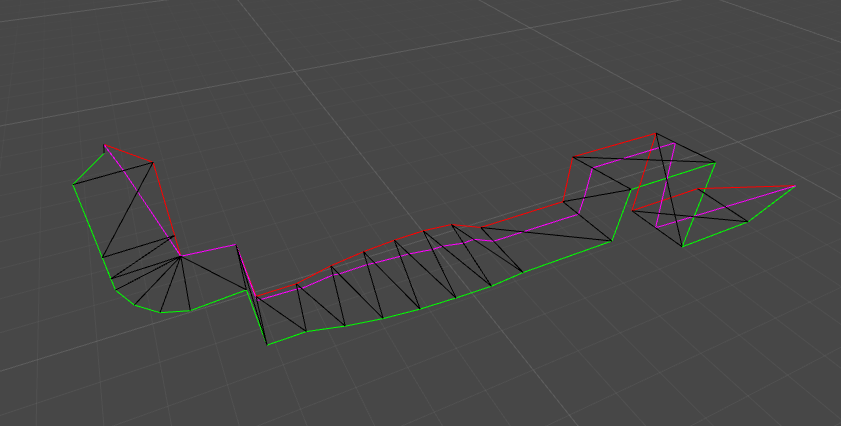The input is a funnel like in the image below. It may be rotated and twisted. The output will be a funnel in 2D space like in the image below. All twists and bends will have been straightened out.

This array is used as a cache and the unwrapped portals are calculated on demand. Thus it may not contain all portals.